「資格試験 難易度」で検索すると、資格試験の難易度を偏差値で数値化して並べているものがいくつか見受けられます。しかしながら、それらに意味はありません。
この記事では偏差値について簡潔に説明します。
読んでいただいた方には、資格試験の難易度を偏差値で語ることがいかにナンセンスなのかご理解いただけます。
偏差値とは?
◆大学受験、高校受験、中学受験などでよく目にする偏差値。
そのもとになるのは標準偏差です。
◆次の表をご覧下さい。
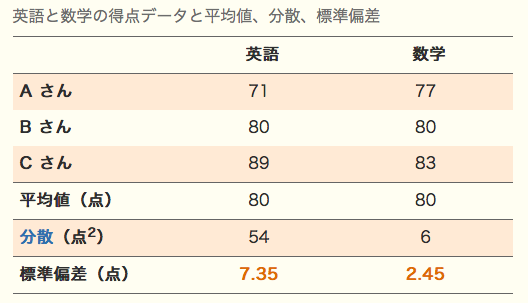
標準偏差についてとてもわかりやすく丁寧に書かれている標準偏差の意味と求め方 - 公式と計算例からの引用です。
この表は、Aさん、Bさん、Cさんという3人が英語と数学の試験を受けた結果です。
ここで大切なのは、英語と数学の両方の試験をAさん、Bさん、Cさんが受けていることです。
つまり、Aさん、Bさん、Cさんという3人による集団をもとに、英語と数学の試験それぞれについて平均値、分散、標準偏差を算出しています。
このとき、「Aさん、Bさん、Cさんという3人による集団」のことを「母集団」と呼びます。
もう一度表をみてください。

同じ母集団(Aさん、Bさん、Cさん)が、英語と数学という、異なる試験を受けました。英語と数学の平均点はどちらも同じ80点ですが、標準偏差は英語が7.35点、数学が2.45点と違いがみられました。
英語と数学での標準偏差の違いはどこからくるのでしょうか?
標準偏差は分散を求めれば計算できます。
分散は偏差を求めれば計算できます。
偏差を求めるには平均点が必要です。
では、まず偏差を計算してみましょう。
偏差を計算してみよう
Aさんの英語の得点は71点です。
英語の平均点は80点なので、その差(偏差)は-9点。
Bさんは平均点と同じなので、偏差は0点。
Cさんの偏差は+9点です。
偏差が計算できたので、次に分散を計算してみましょう。
分散を計算してみよう
各人の英語の偏差を二乗して和を求めると、162になります。これを3で割る(3人なので)と54点²になります。これが分散です。
一方、3人それぞれの数学での偏差は英語より小さいことがすぐに見てとれます(Aさんの偏差は-3点、Bさんは0点、Cさんは+3点)。各人の偏差を二乗して和を求めると18、これを3で割ると6点²になります。
- 英語の分散は54点²
- 数学の分散は6点²
これで分散の値が計算できました。
英語の得点は18点以内、数学の得点は6点以内に3人それぞれが位置していますね。つまり、英語の得点のほうが、数学の得点よりもばらついてると言えます。
そう、分散とは数値のばらつき具合を示す値なのです。
ただし、今回用いた英語と数学の「点」という単位でいえば、分散は計算に「二乗」が入ることから単位は「点²」となっています(上の表も参照)。
そこで、単位を「点」にそろえるため、分散の正の平方根を計算します。実は、これこそが標準偏差なのです。
標準偏差を計算してみよう
標準偏差は分散の正の平方根で求められます。
英語の標準偏差は分散(54点²)の平方根、すなわち≈7.35点(小数点第2位まで表示)。
数学の標準偏差は分散(6点²)の平方根、≈2.45点(小数点第2位まで表示)となります。
分散は「数値のばらつき具合を示す値」と述べました。もちろん、標準偏差も「数値のばらつき具合を示す値」です。そして、標準偏差は分散と違って計算もとの数値と単位をそろえてあるのです。 より使いやすい数値なのです。
◆このように、平均値、偏差、分散、標準偏差を算出することで、英語と数学の平均点をくらべるだけでは決して目に見えてこない得点のばらつき具合の違いがわかるのです。
同じ母集団で違う科目の試験を受けたとき、平均値(点)が同じでもどちらかの標準偏差のほうが大きければ、それだけ得点のばらつきが大きかったことになります。
そして、冒頭で述べた通り、標準偏差は偏差値のもとになります。というのは、偏差値とは「自分の得点から平均値を引いた値を標準偏差で割って10倍し、それに50を加え(偏差値とは何か? - 偏差値の意味と求め方より)」たものだからです。
自分の得点が平均点と同じなら偏差値は50になる
では実際に偏差値を計算しましょう(小さい母集団ではありますが、偏差値の計算を実感するためにそのまま用います)。
まず、わかりやすいBさんからみてみます。
◆Bさんの得点は英語も数学も80点、平均点は英語も数学も80点です。
- Bさんの英語の偏差値=(80-80)/7.35×10+50=0+50=50
- Bさんの数学の偏差値=(80-80)/2.45×10+50=0+50=50
このように、自分の得点が平均点と同じなら偏差値は50になります。逆に言えば、ある試験で偏差値50だったら、それはその試験の平均点と同じだった、ということになります。
ではAさんについても偏差値を計算しましょう。
◆Aさんの得点は英語71点、数学77点、平均点は英語・数学ともに80点です。
- Aさんの英語の偏差値=(71-80)/7.35×10+50=-12.2+50=37.8
- Aさんの数学の偏差値=(77-80)/2.45×10+50=-12.2+50=37.8
最後にCさんの偏差値を計算しましょう。
◆Cさんの得点は英語89点、数学83点、平均点は英語・数学ともに80点です。
- Aさんの英語の偏差値=(89-80)/7.35×10+50=-12.2+50=62.2
- Aさんの数学の偏差値=(83-80)/2.45×10+50=-12.2+50=62.2
英語と数学で得点に違いがあるにもかかわらず、Aさんは英語・数学ともに偏差値37.8、Cさんも英語・数学ともに偏差値62.2となりました。
3人の英語・数学の試験結果の偏差値はこうなりました。
- Aさん:英語・数学ともに偏差値37.8
- Bさん:英語・数学ともに偏差値50
- Cさん:英語・数学ともに偏差値62.2
Bさん以外の二人は英語と数学の得点が違います。でも、偏差値は二人とも英語・数学で一緒です。
これは、偏差値もばらつきを示しているからなのです。なにしろ、偏差値は「自分の得点から平均値を引いた値を標準偏差で割って10倍し、それに50を加えたもの」なのですから。
偏差値とは?
偏差値は1960年代中頃、東京都公立中学教師だった桑田昭三氏によって学力評価の一指標として考案されました(http://hosted.jalt.org/test/PDF/Kuwata-j.pdf)。
偏差値60とか70だと何かものすごく良い印象をもってしまいます。
しかしながら、偏差値とは、ある試験における得点が、その試験においてどの位置に分布するのか?を示す値にすぎないのです。
◆偏差値の最大の特徴は、ある試験における平均点が偏差値50になるよう操作されていることです(偏差値は「自分の得点から平均値を引いた値を標準偏差で割って10倍し、それに50を加えたもの」)。
得点分布が正規分布する場合、試験の偏差値が70以上なら、それは全体の上位2.275%に入っていることを意味します。偏差値60以上なら上位15.865%に入っています。偏差値50なら上位50%以内に入っています。
偏差値とは何か? - 偏差値の意味と求め方にはこう書いてあります。
偏差値とは、テストの得点などの数値が、集団の平均値からどの程度へだたっているのかを示す数値です。
自分の点数が平均点と同じであれば、偏差値は必ず 50 となります。偏差値 50 を基準にして、平均点よりも高い得点なら、偏差値は 50 よりも大きくなり、逆に平均点よりも低い得点なら、偏差値は 50 よりも小さくなります。
一般的なテストにおいて、ほとんどの人の偏差値は 25 ~ 75 の範囲に収まります。すなわち、偏差値 70 ~ 75 程度であれば「非常に成績が良い」といえ、逆に偏差値 25 ~ 30 程度であれば「非常に成績が悪い」といえます。
◆資格試験で言えば、宅建試験の合格率は約15%です。だからと言って、宅建試験の偏差値を60くらいと言っても良いのでしょうか?
思い出して下さい。
偏差値を計算するには標準偏差が必要です。
標準偏差の計算には分散が必要です。
分散の計算には偏差が必要です。
偏差の計算には平均点が必要です。
では、宅建試験の合格率はどのようにして計算されているのでしょうか?
もちろん合格者数÷受験者数です。そこには平均点も偏差も分数も標準偏差も、まして偏差値の計算も登場しません。
繰り返します。
ある試験の平均点は、その試験の問題と、その試験を受けた受験生によって決まります。
したがって、同じ試験問題であっても、受験生(母集団)が違えば平均点・偏差・分散・標準偏差が違い、結果として偏差値は別物になります。
◆良い例がファイナンシャル・プランニング技能検定(以下、FP試験)です。
FP試験の実施団体は一般社団法人金融財政事情研究会(きんざい)と日本FP協会があります。試験には学科試験と実技試験があり、学科試験はどちらも同じ問題を用いています。もちろん学科試験の合格点は同じです(60点満点で36点)。
しかしながら、学科試験の問題が同じなのにもかかわらず、きんざいと日本FP協会での合格率はぜんぜん違います。
ちなみに2018年5月実施2級FP試験の合格率はきんざい28.53%に対し、日本FP協会は45.63%。同じ問題を解いているにもかかわらず合格率がこれほど違うのは、母集団が違うためです。
ところで、きんざいと日本FP協会のFP2級学科試験の偏差値を比べることに意味はあるでしょうか?
いいえ、ありません。
違う母集団の間で偏差値を比較しても意味はないのです。
偏差値は、(それを計算するための)同じテストを受けた集団の中で、自分がどの程度の位置にいるかを示す指標です。よって、同じ集団の中で異なるテストの比較をする際には有用ですが、集団が異なるテストの結果を偏差値で比べることはできません。
例えば、全国で行われる模試と、自分の学校の中だけで行われる模試の2つがあったとしましょう。この場合、この2つの模試は集団が異なっているため、偏差値を使って直接結果を比べることができません。(偏差値とは何か? - 偏差値の意味と求め方)
繰り返します。同じ試験問題であっても母集団が違えば結果を直接比べることはできません。
まして、母集団のみならず試験問題すら違っているのであれば、「偏差値」を比べることなどできるはずもありません。
ここまで言えば読者の皆様もお気づきのように、
違う資格試験同士の偏差値を並べてもなんにもならない
のです。誰にでもおわかりいただけると思いますがいかがでしょうか?
偏差値の計算には手順が必要です。
手順を踏まずに、あるいは手順をチェック・追試できるよう開示しないまま「独自の計算」などと言って偏差値を「表示」したところで、それは偏差値でもなんでもありません。
試験実施団体が情報を開示していない限り、他団体や業者、あるいは個人が偏差値を算出できるはずがないのですから。
まとめ:資格試験の難易度を偏差値で比較するのは極めてナンセンスである
各種資格試験を偏差値でランク付けしている記事は、「試験の合格率をただ単に偏差値の正規分布に当てはめたにすぎない」ものと思われます。
それは偏差値ではありません。
この手法で先に紹介した2018年5月実施FP2級学科試験合格率を「自称偏差値」(「フェイク偏差値」「似非偏差値」「偽偏差値」「嘘偏差値」)に換算すれば、きんざい実施分は偏差値55〜56の間、日本FP協会実施分は偏差値51〜52の間になります。
ですが、これらは偏差値ではありません。
仮に実施団体が試験結果データに基づいて偏差値を算出したとしても、きんざい・日本FP協会という「集団が異なるテストの結果」を偏差値で比べることはできないのですから。
まして異なる資格試験同士の偏差値を比べるなどできるはずもありません。極めてナンセンスなのです。
このエントリーを読んでいるあなたが、ある資格試験を受けようとして、その難易度を複数の試験の間で比べるのに偏差値を参考にしようとするなら、即刻やめることを強く薦めます。
耳慣れた「偏差値」の計算方法を今一度確かめて、誤用・誤解することのないよう、くれぐれもご注意ください。
